Research

2025	Algebraic geometry of rational neural networks	arXiv
with Elina Robeva, Maksym Zubkov
2025	Identifiability through special linear measurements	arXiv
with Fulvio Gesmundo, André Uschmajew	How many linear measurements do we need to uniquely identify a point on a variety? It turns out that for generic measurements the answer is dimension-many plus one.
2024	Rational Maximum Likelihood Estimators of Kronecker Covariance Matrices	arXiv, journal
with Mathias Drton, Andrew McCormack	Matrix-variate data appearing in applications often exhibit high correlations among rows and columns. A model for such data posits a Kronecker product structure on the covariance matrix, leading to a significant decrease in dimensionality. We use algebraic and symbolic methods to find rational solutions for the maximum likelihood estimation problem and study the ML degree.
2023	Algebraic Sparse Factor Analysis	arXiv, mathrepo, journal
with Mathias Drton, Irem Portakal, Nils Sturma	Factor analysis is a tool to reduce complexity by explaining correlations among random variables as linear functions of fewer hidden variables called factors. In statistical reality a latent variable will only affect a subset of the observed ones, leading to sparsity structures.In this work we study the dimension of the model, provide equations for the entries of the covariance matrices and give a delightful strategy to compute Gröbner bases.
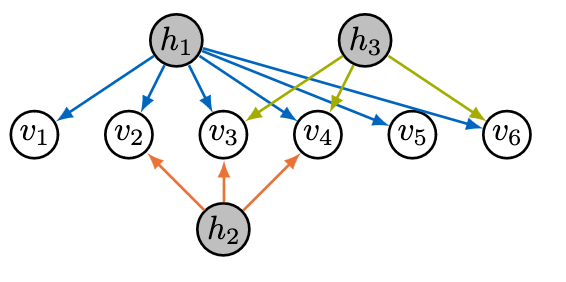2023	Parametric and nonparametric symmetries in graphical models for extremes	arXiv, github
with Frank Röttger, Jane Ivy Coons	Colored graphical models provide a parsimonious approach to modeling high-dimensional data by exploiting symmetries in the model parameters. Thanks to a stability property of the multivariate Pareto distributions, colored extremal tree models can be defined fully nonparametrically. For general graphs, the parametric family of Hüsler-Reiss distributions allows for two alternative approaches to colored graphical models. We study both model classes and introduce statistical methodology for parameter estimation. It turns out that for Hüsler–Reiss tree models the different definitions of colored graphical models coincide. In addition, we show a general parametric description of extremal conditional independence statements for Hüsler–Reiss distributions. Our methodology outperforms existing approaches on real data.
2021	Third-Order Moment Varieties of Linear Non-Gaussian Graphical Models	arXiv, repo, journal
with Carlos Améndola, Mathias Drton, Roser Homs, Elina Robeva	A directed graph corresponds to a statistical model where the nodes represent random variables and arrows encode relations between them. The polynomial relations between entries of the covariance matrices have been previously studied from an algebraic and combinatorial point of view. Dropping Gaussianity makes moment tensors of higher order meaningful. Extending the combinatorial description from covariance matrices to higher-order tensors, we can use computational algebra to obtain a description for the third-order moment variety for trees. We also describe the polytopes coming from the moment parametrisation and explain the situation for graphs with hidden variables.
2020	Exact Solutions in Log-Concave MLE	arXiv, journal, github
with Kaie Kubjas, Olga Kuznetsova, Alexander Heaton, Georgy Scholten, Miruna-Stefana Sorea	In nonparametric statistics one abandons the requirement that a probability density function belongs to a statistical model. Given a sample of points, we want to find the best log-concave distribution that fits this data. This problem was originally studied by statisticians, who found that the optimal solutions have probability density functions whose logarithm is piecewise-linear and used numerical methods to approximate the pdf. In this work we use algebraic and combinatorial methods to provide exact solutions to this problem. At the same time we use tools from algebraic geometry to test if the solutions provided by statistical software can be certified to be correct.How many regions of linearity does the depicted tent function have?
2018	Moment ideals of local Dirac mixtures	arXiv, journal
with Markus Wageringel	Algebraic methods can find wide use in parameter estimation from statistical moments. In this work we use tools from elimination theory, the extended Prony method, and numerical algebra to reconstruct parameters from mixtures of local Diracs. Computational algebra mixes successfully with applications in statistics and signal processing.The picture shows the moment hypersurface of a first order local Dirac mixture, i.e. the variety parametrized by the moments. It is the tangent to the twisted cubic, in the same way that regular mixing gives rise to secants.

Share this: